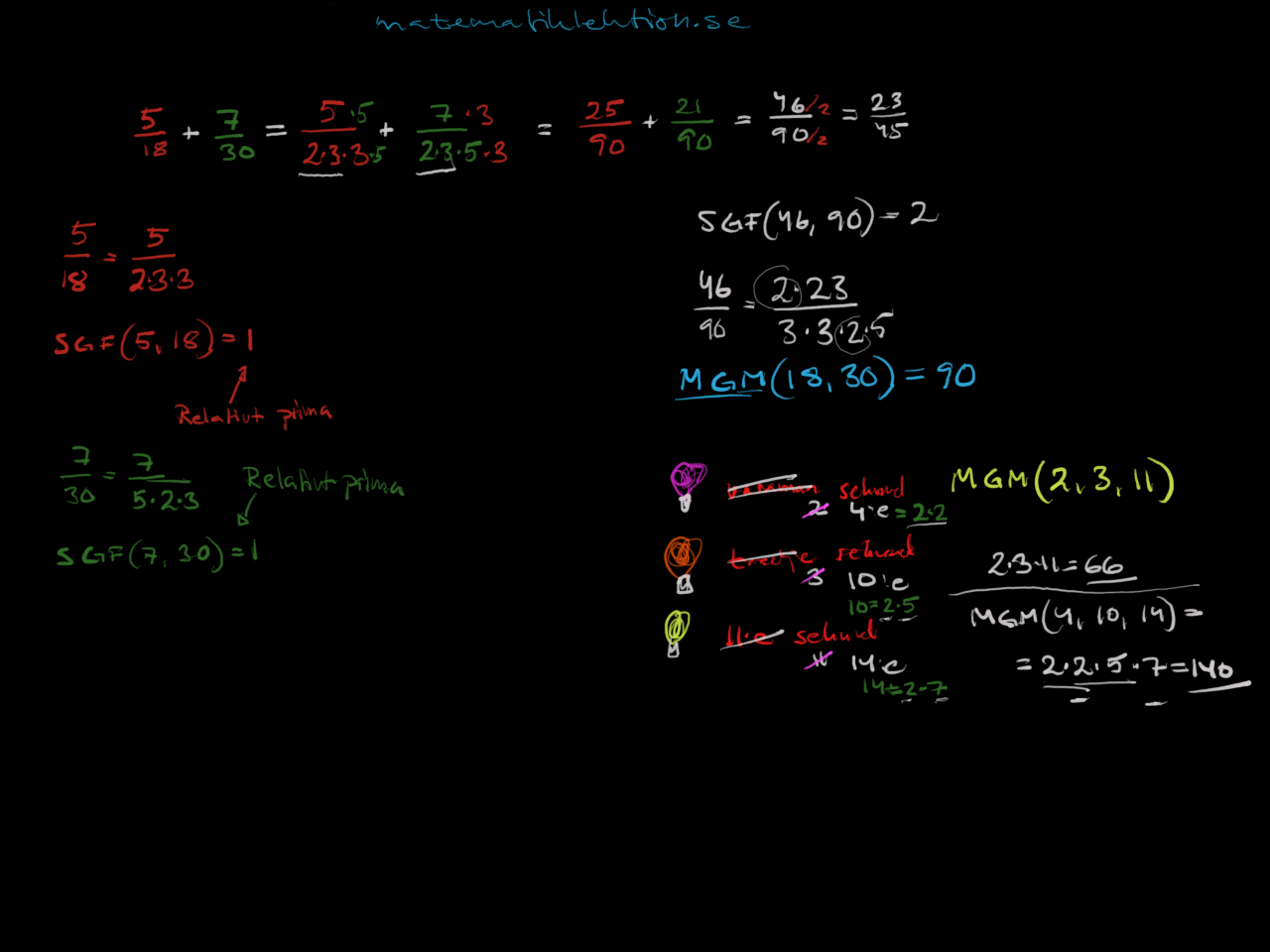Filmen tar upp begreppet modulo och kongruens inom aritmetik. Aritmetik betyder egentligen bara vanlig räkning, sådan man gör inom låg- och mellanstadiet. Uppställningar och de fyra räknesätten är centrala inom aritmetik. Modulär räkning kräver en ...
Read More »Gemensamma och icke-gemensamma faktorer (MGM & SGF)
Filmen tar upp begrepp som minsta gemensamma multipel och största gemensamma faktorer (delare). Centralt är kunskapen om primtalsfaktorisering. Du kan göra dessa beräkningar även på räknaren med verktygen gcd och lcm. [ratings]
Read More »Erathostenes såll
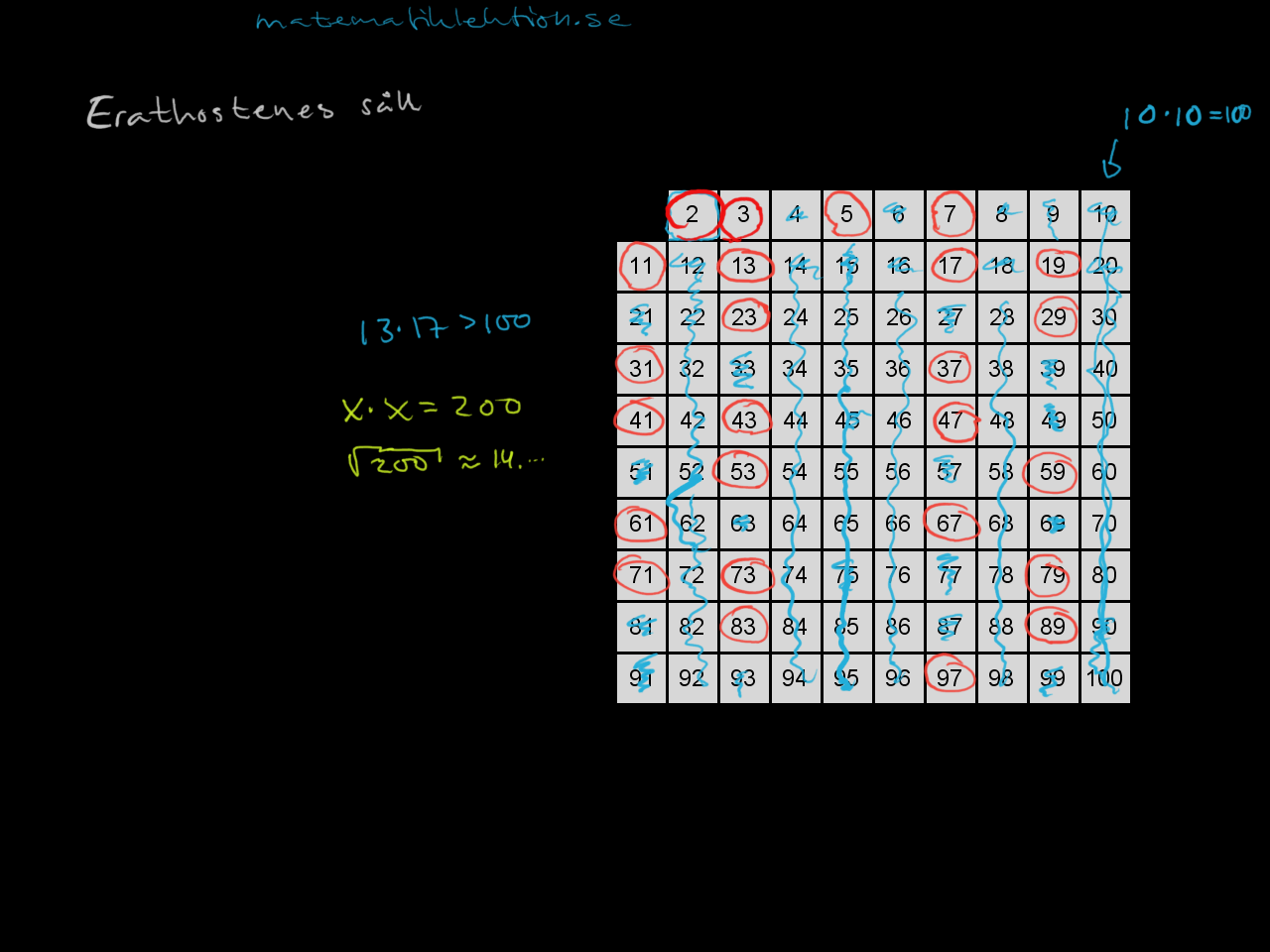
Erathostenes såll är en enkel metod för att fastställa vilka tal som är primtal. En gammal och enkel metod. Det kan tillhöra en matematisk allmänbildning att kunna använda sig av Erathostenes såll. [ratings]
Read More »Primtal och delbarhet, en fördjupning
Här är en fördjupning kring begreppet primtal. Jag rekommenderar dig starkt att skapa dig en förståelse kring vad primtal är och hur de används. De kommer att effektivisera ditt räknande. [ratings]
Read More »Primtal och delbarhet
Primtalens betydelse är viktig dels inom forskningen kring datasäkerhet och kryptering men även för att förstå hur man ska förlänga bråktal för att de ska få en gemensam nämnare. Primtal används överallt och om du ...
Read More »Proportioner
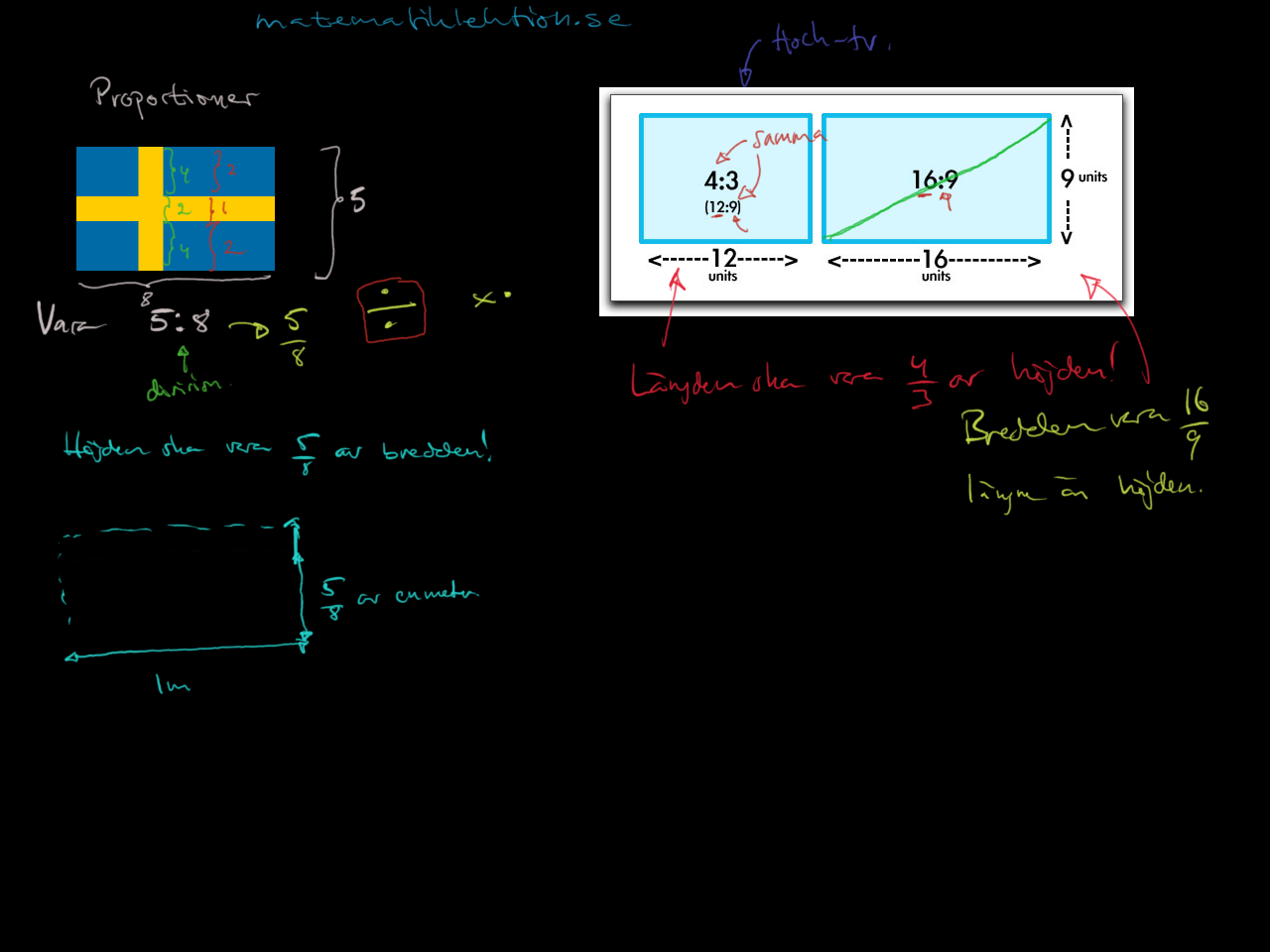
Det är vanligt att man anger mått i proportioner. TVns proportioner kan anges som 16:9, saft blandas 4+1 (skrivs då 4:1). Inom skolan tar man om IT-satsning som 1:1. Detta betyder förhållandet mellan olika delar. ...
Read More »Komplexa tal som vektorer
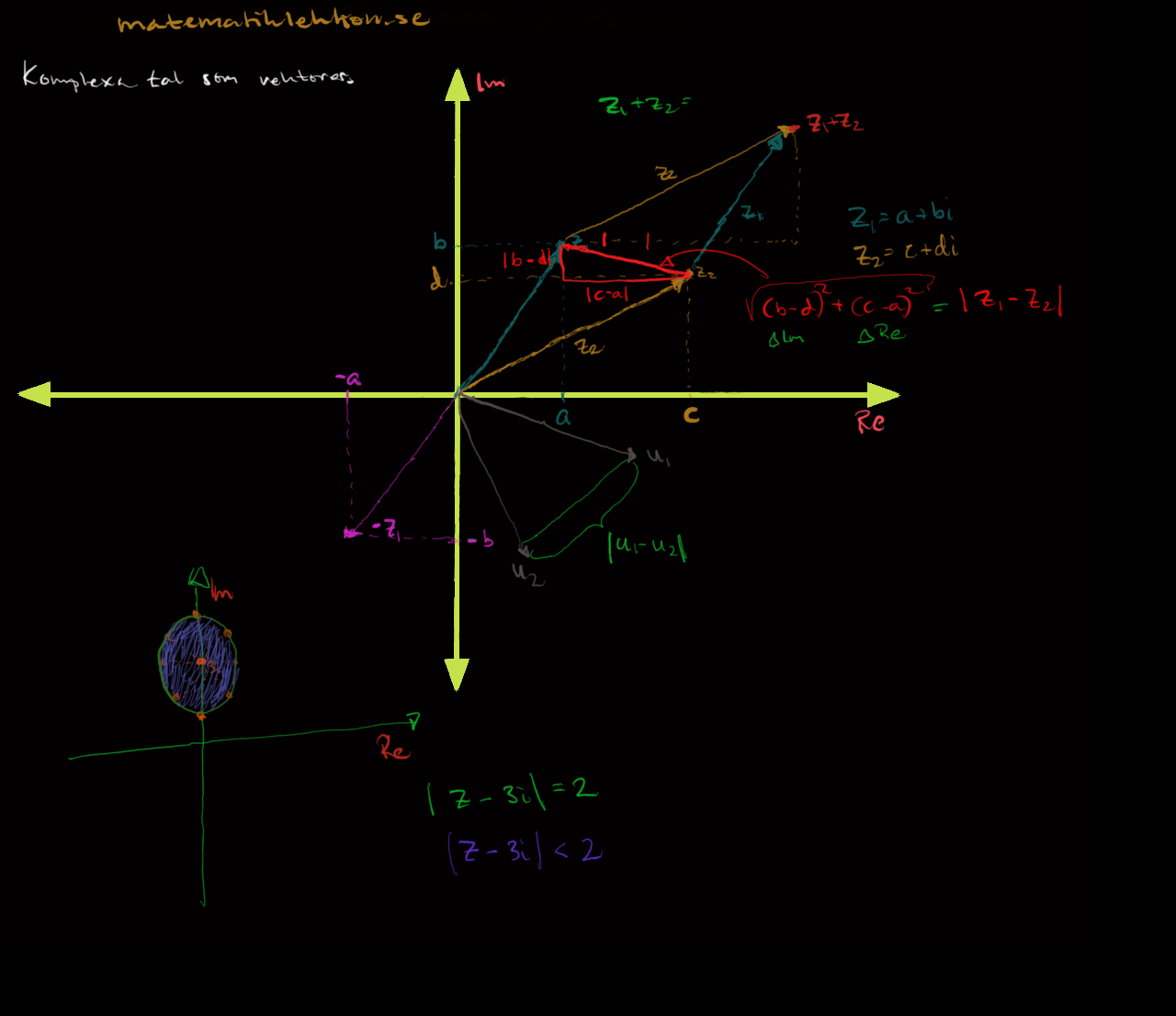
Ett fysikaliskt sätt att behandla komplexa tal är att se dem som vektorer. Det kommer att underlätta räkningen av växelström bland annat. [ratings]
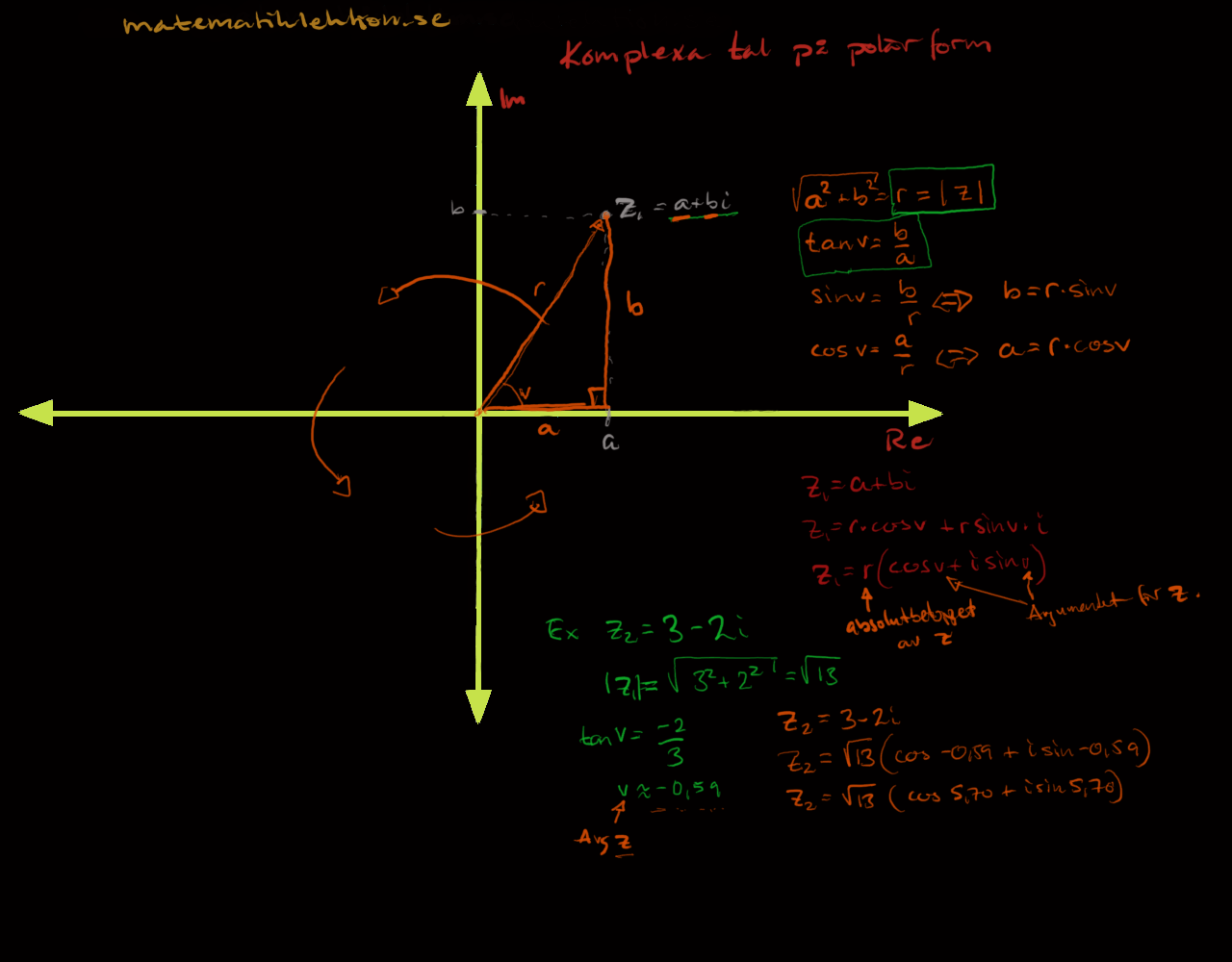
Read More »Komplexa tal på polär form
Komplexa tal kan skrivas på formen a+bi men även i polär form. Båda sätten har sina fördelar även om polär form till en början kan ses som väldigt invecklad. Det visar sig senare att polär ...
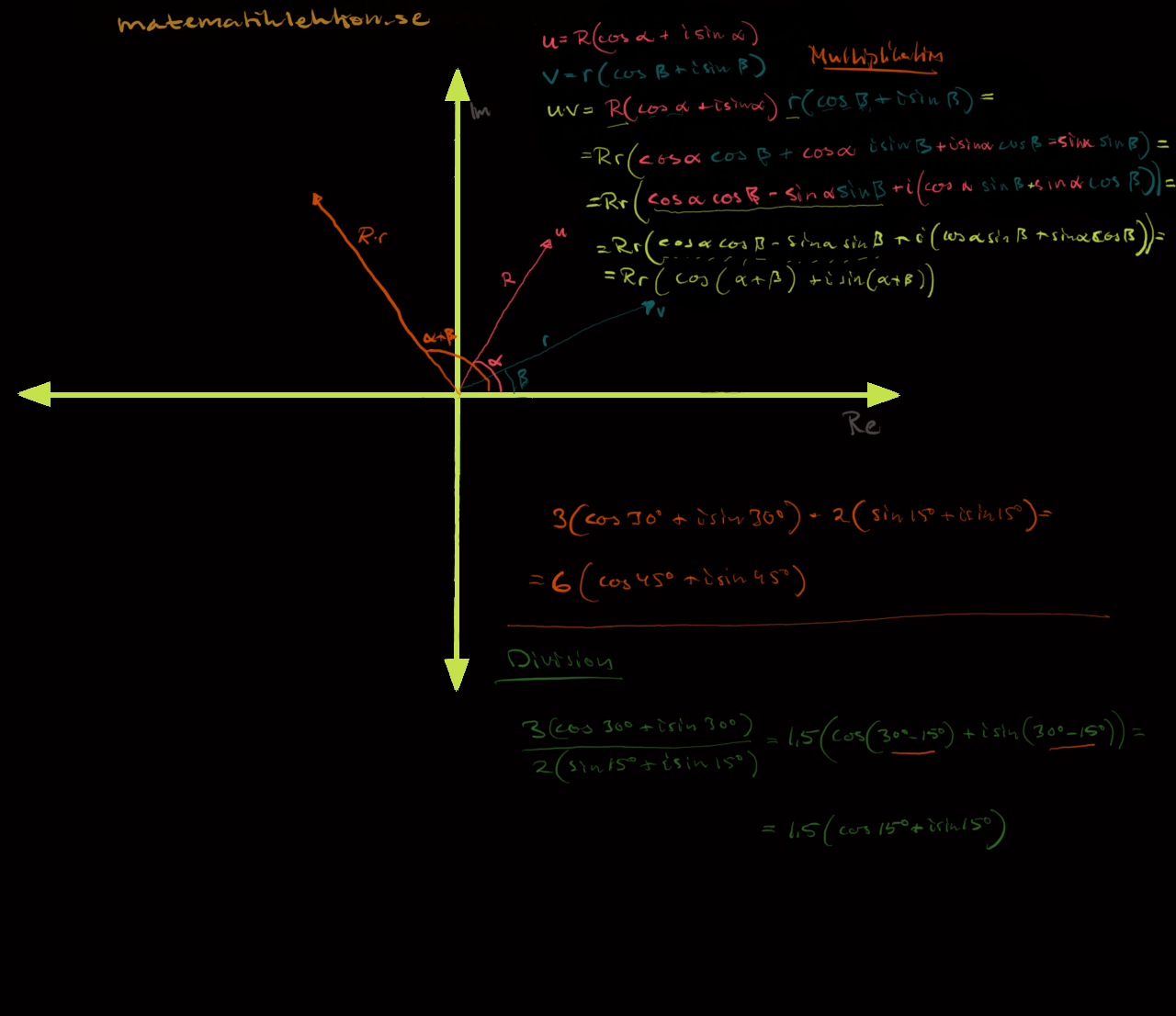
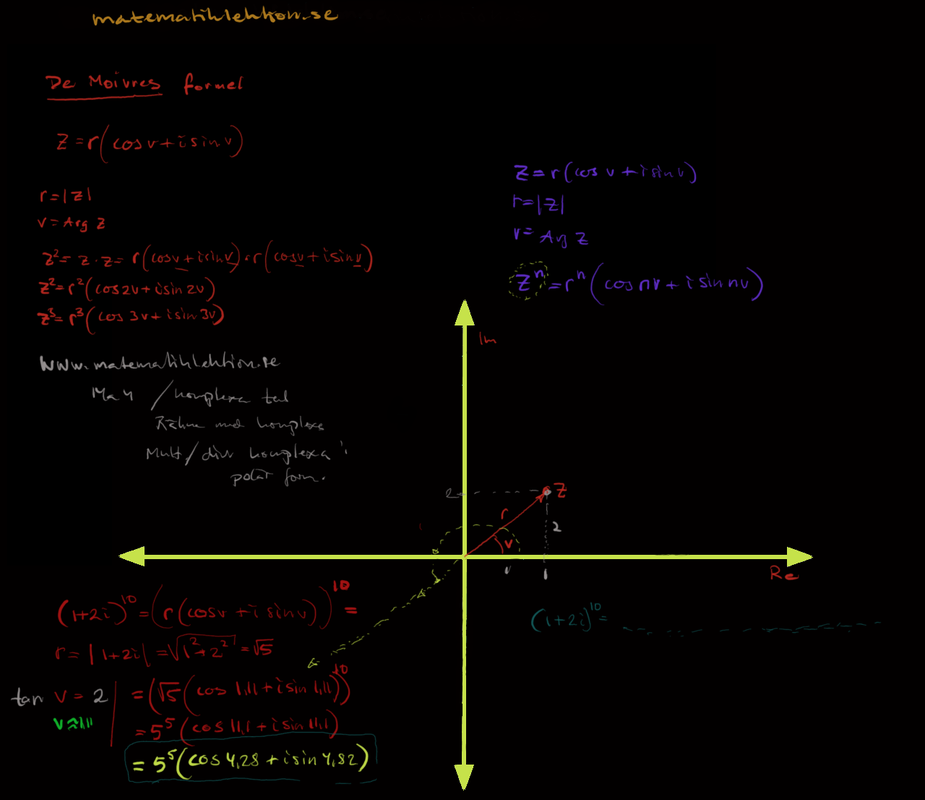
Read More »Multiplikation och division med komplexa tal i polär form
Addition och subtraktion görs bäst när komplexa tal är skrivna på formen a+bi men både division och multiplikation går utmärkt att göra i polär form. Bättra än så faktiskt. Det är lättare att förstå vad ...
Read More »Kurvan till y = sin x + cos x
Kurvan till addition mellan sinus och cosinus ser ut som gråfen till en helt vanlig sinusfunktion, fast förskjuten; flyttad i sidled. Så naturligtvis går det att skriva om addition av sinus och cosinus som en ...
Read More »