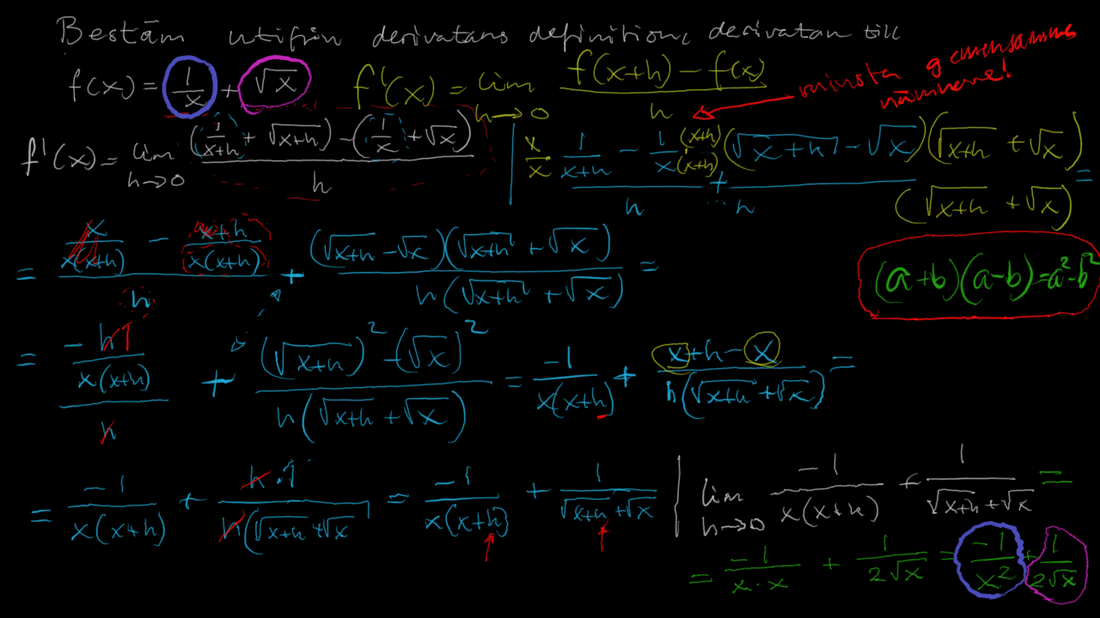
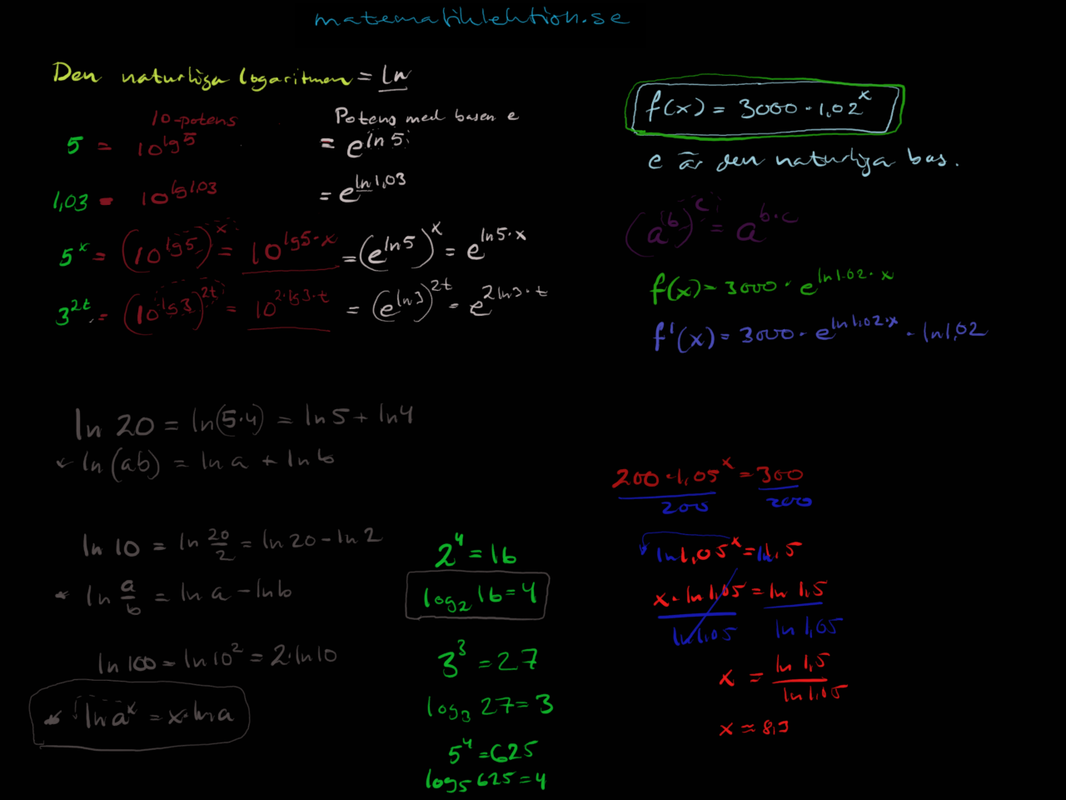För att förstå derivata måste man blanda in något oändligt lite, eller 2 punkter som är oändligt nära varandra, det vill säga att avståndet mellan punkterna är oändligt nära noll. Rent matematiskt använder man sig ...
Read More »Ma3: Rita grafer med räknaren TI-82
Filmen beskriver hur man ritar grafer med Texas Instrument TI-82. Tar även upp hur man justerar koordinatsystemet, hur man finner koordinaterna för skärnings- och max/min-punkter samt bestämmer derivatan i olika punkter. [ratings]
Read More »Härleda derivatan ur derivatans definition ur ett svårare exempel, en tredjegradsfunktion
Här härleds derivatans ur en allmän tredjegradsfunktion. I princip är det samma metod som man använder för enklare funktioner men här gäller det att hålla koll på alla siffror och bokstäver, det blir lätt många. ...
Read More »Härleda derivatan ur derivatans definition ur en allmän andragradsfunktion
Det här avsnittet bör du redan ha lärt dig men det skadar inte att repetera. [ratings]
Read More »Test på derivata och ändringskvot
Ett test för att du ska kunna avgöra ifall du har förstått kapitlet om derivata och ändringskvoter. Läser in… [ratings]
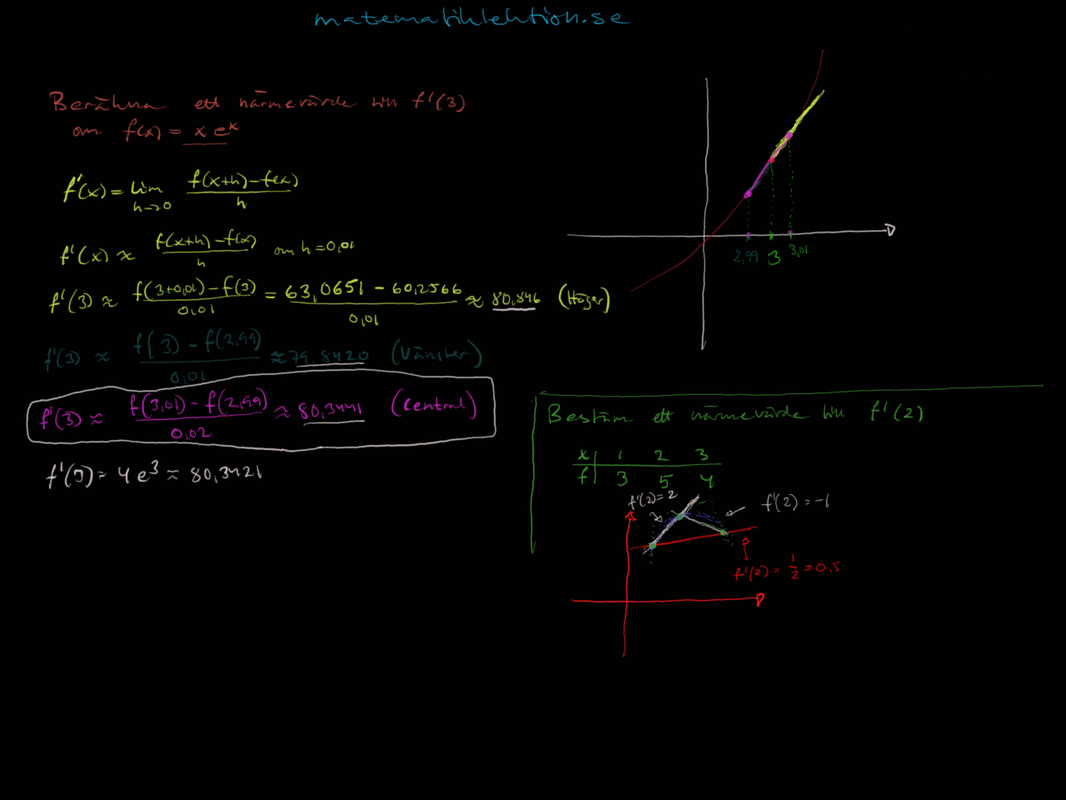
Read More »Närmevärde till derivata – differenskvot
En del funktioner går inte att derivera med hjälp av de deriveringsregler som du lärt sig. Exempel på det är när man multiplicerar ihop delar som vardera lyder under olika regler. T.ex.: \[f(x)=x \cdot e^{2x} ...
Read More »Derivera en godtycklig exponentialfunktioner när basen inte är e.
Så om man inte har basen e då? Då behöver du göra om basen, alltså byta basen för potensen. Filmen visar hur du ska göra det, hur du ska derivera den sedan och vad resultatet ...
Read More »Den naturliga logaritmen ln
Filmen visar hur man skriver om exponentialfunktioner med valfri talbas till basen e. Detta måste göras för att kunna derivera funktionen, det endast exponentialfunktioner med den naturliga basen e som man kan använda derivataverktyget. \[f(x)=200 ...
Read More »Derivatan av en exponentialfunktion och det magiska talet e
Filmen visar hur man får fram derivatan av en exponentialfunktion. Längs vägen dyker det magiska talet e upp som en nödvändighet för att derivera exponentialfunktionen. I slutet ges några exempel på hur man deriverar en ...
Read More »Derivatan av en potensfunktion
Att bevisa derivatan för polynom när x endast är upphöjt till positiva heltal är inget svårt. Att göra detsamma för när x är upphöjt till vilket tal som helst, även negativa och bråktal, är knepigare. ...
Read More »