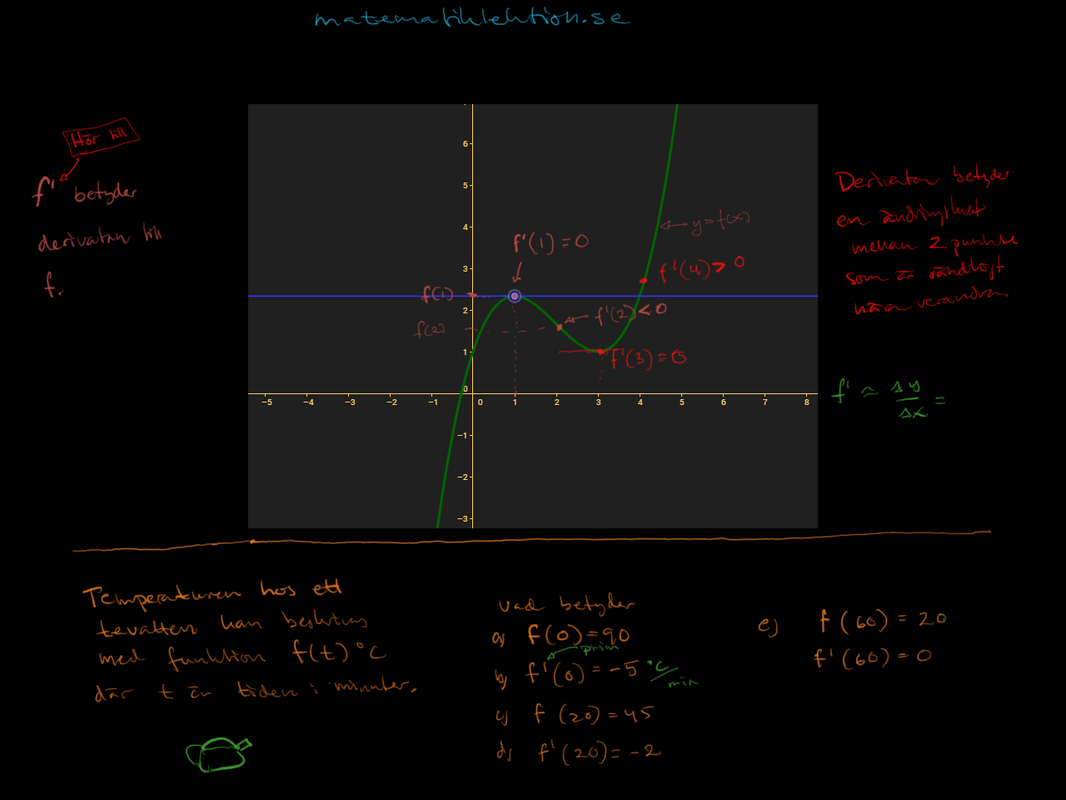
Egentligen kan man inte säga att det finns en lutning i en punkt. Det vore som att säga att en bil rör sig i ett ögonblick och det vet du, om du tänker dig en ...
Read More »
Tangent och begreppet "derivata"
Här ligger fokus på att förstå hur begreppet tangent fungerar. Kortfattat kan man säga att en tangent är en rät linje som får igenom en punkt på en graf och som har samma lutning som ...
Read More »
Ändringskvot och derivata
Begreppen ändringskvot och sekant hör ihop och under kursens gånger kommer du säkert att glömma bort dessa två begrepp när du lär dig vad derivata är för något. Det är dock viktigt att du återkommer ...
Read More »
Cosinussatsen
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 49
Cosinussatsen kan sägas vara en justering av den vanliga pythagoras sats. Jämför pythagoras sats med cosinussatsen nedan Cosinussatsen är bl.a. väldigt användbar när man inte känner till någon vinkel alls i en triangel. [ratings]
Read More »
Sinussatsen
Sinussatsen är det ena kraftfulla verktyget av två för att kunna beräkna en godtycklig triangels alla sidor och vinklar. Den är relativt okomplicerad att använda men den kan vara besvärlig när det gäller att tolka ...
Read More »
Areasatsen (2 filmer)
Och del 2
Read More »
Cirkelns ekvation, enhetscirkeln och några trigonometriska samband
Det går inte att underskatta betydelsen av att förstå hur enhetscirkeln och de trigonometriska funktionerna hänger samman. Det är otroligt viktigt att du förstår hur enhetscirkeln avgör hur många lösningar en trigonometrisk ekvation har inom ...
Read More »
Några standardtrianglar som ger vissa värden för sinus och cosinus
De här två trianglarna, den räta & likbenta samt en halv liksidig triangel ger vissa förutbestämda värden för sinus och cosinus med vinklarna 30°, 40° och 60°. Dessa värden behöver du inte kunna, det räcker ...
Read More »
Faktorsatsen
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /customers/2/2/b/matematiklektion.se/httpd.www/wp-content/plugins/latex/latex (2).php on line 49
Faktorsatsen används för att kunna faktorisera polynom med hjälp av dess nollställen. Om man har ett polynom så kan man hitta dess nollställen genom att lösa ekvationen med hjälp av PQ-formeln. Då får man lösningarna: ...
Read More »